3.2. Example: 38 Lennard-Jones Particles
Tip
The sample input and output files can be found in testfiles/atom/1-lj38.
The system here is composed of 38 particles interacting with Lennard-Jones potential. We want to find its global minimum.
Step 1: call abcinp to generate input files:
$ abcinp lj38 1 LennardJones 5.0 30 300 5 30 38 C
Parameters for atom 0: sigma epsilon > 1.4 1.0
This meaning of arguments of abcinp is explained Build atom Input. You will see that three files are generated: lj38.inp, lj38.par, and lj38i.xyz
Step 2: Run the global optimization:
$ atom lj38.inp > lj38.out
After a few seconds, you will find several new files:
lj38.outThe main output file.lj38.xyzThe global minimum in XYZ format. It can be read by for example, VMD, CYLView, or VESTA.lj38.gjfThe global minimum in Gaussian input format. It can be read by for example, GaussView.lj38-LMA folder containing all local minima, each one having two files in XYZ and Gaussian input format, respectively. They are sorted in energy-increasing order, for example,0.xyzis lower in energy than13.xyz.abcluster*.xyz/gjfThe file containing the currently found global minimum during the running ofatom. You can check the current stable structure beforeatomterminates. It it crashes, one can use thisabcluster*.xyzto start a new optimization.
Now, you can check the global minimal energy in lj38.out:
-- Results Report --
* 30 LMs will be saved in [ lj38-LM ].
# Energy Match-RMSD
0 -173.92842659 0.00000000
1 -173.25237842 0.71507423
2 -173.13431701 0.70945024
3 -172.95863341 0.76108783
4 -172.87773641 0.76045325
5 -172.23492649 0.74732850
6 -172.23071016 0.73688291
7 -172.22667896 0.73840467
8 -171.86939588 0.72369028
9 -171.85602243 0.69971268
10 -171.79229098 0.83970678
11 -171.75808589 0.71170034
12 -171.69540490 0.69620306
13 -171.64009388 0.67759186
14 -171.50996865 0.76198085
15 -171.44256681 0.69102789
16 -171.43424502 0.65131617
17 -171.38576546 0.66268896
18 -171.35733954 0.76830008
19 -171.34259018 0.68397072
20 -171.32073147 0.75987386
21 -171.29716664 0.67851866
22 -171.27902087 0.69044599
23 -171.20726248 0.86629661
24 -171.18001445 0.78347207
25 -171.14751710 0.76899129
26 -171.13754901 0.70110475
27 -171.11143840 0.77154060
28 -171.10452382 0.64102747
29 -171.09481231 0.77978973
* Final Global Minimal Energy : -173.92842659
* The Global Minimum is saved as: [ lj38.(gjf/xyz) ]
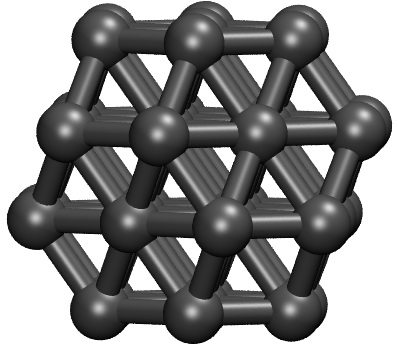
The energies and RMSDs relative to lj38-LM/0.xyz of 30 local minima are listed. Their geometries are stored in lj38-LM. The geometry of the global minimum is lj38.xyz or lj38-LM/0.xyz. This global minimum is visualized below. It is a face-centred-cubic truncated octahedron cluster.