3.4. Example: (MgO)20

Tip

The sample input and output files can be found in testfiles/atom/2-mgo20.

The system here is \(\left(\mathrm{MgO}\right)_{20}\) interacting with Coulomb-Born-Mayer potential. The parameters for \(\mathrm{Mg}\) and \(\mathrm{O}\) can be found in misc/atomic-force-field.txt:

misc/atomic-force-field.txt
Metal-Metal     0.000    0.1       #  J. Phys. C 1985, 18, 1149
O (-2)-O(-2)    22746    0.149     #  J. Phys. C 1985, 18, 1149
Mg(+2)-O(-2)    821.6    0.3242    #  J. Phys. C 1985, 18, 1149

This suggests that these parameters are taken from the paper J. Phys. C 1985, 18, 1149. The parameters are ordered exactly the one that abcinp needs. Just simply copy them to abcinp.

Step 1: call abcinp to generate input files:

$ abcinp mg20o20-q2 2 CoulombBornMayer 5.0 100 100 5 30 20 Mg 20 O
Parameters for atom 0: q > +2
Parameters for atom 1: q > -2
Parameters for atom-pair 0-0: B rho > 0.0 0.1
Parameters for atom-pair 0-1: B rho > 821.6 0.3242
Parameters for atom-pair 1-1: B rho > 22746 0.1490

Here, atom 0 and atom 1 stand for \(\mathrm{Mg}\) and \(\mathrm{O}\), respectively, being consistent with your input order. Based on Build atom Input, this input means that set \(SN\) = 100, \(g_\mathrm{max}\) = 100, \(g_\mathrm{limit}\) = 5, \(L\) = 5.0. The input and output files are called mg20o20-q2* and 30 local minima will be saved. There are 2 kinds of atoms: 20 Mg and 20 O.

Step 2: Run the global optimization:

$ atom mg20o20-q2.inp > mg20o20-q2.out

After a few seconds, you will find the global minimum in mg20o20-q2.xyz (see below) and local minima in mg20o20-q2-LM.

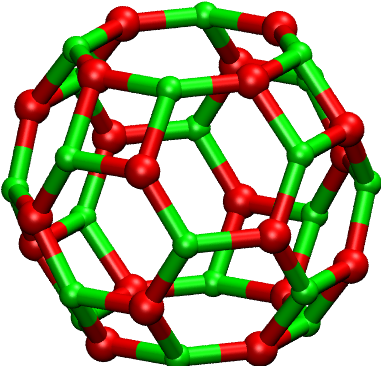
alternate text

You may wonder what the cluster will look like if the formal charges of \(\mathrm{Mg}\) and \(\mathrm{O}\) are +1 and -1, respectively. This can be done by just changing the input of abcinp:

$ abcinp mg20o20-q1 2 CoulombBornMayer 5.0 100 100 5 30 20 Mg 20 O
Parameters for atom 0: q > +1
Parameters for atom 1: q > -1
Parameters for atom-pair 0-0: B rho > 0.0 0.1
Parameters for atom-pair 0-1: B rho > 821.6 0.3242
Parameters for atom-pair 1-1: B rho > 22746 0.1490

and then re-run the global optimization:

$ atom mg20o20-q1.inp > mg20o20-q1.out

You can find the global minimum below. Instead of the hollow cage cluster, the cluster becomes a rocksalt-like one.

alternate text