5.4. Clusters with Specific Point Group Symmetry
5.4.1. Point Group Input
ABCluster can generate atomic clusters with specific point group symmetry. This can be done by just changing the third line of isomer input by point group descriptions. The grammar is:
1name x y z plane(optionally for Cnh, Dn, Dnh, Dnd)
Here, name is the point group name, like C2v, Oh (See below for a full list). x y z are three real numbers. They control the shape of the cluster. For example, 2 2 2 may result a cluster having close length, width, and height, and 5 5 1 may result an elongate cluster. For Cnh, Dn, Dnh, and Dnd, you can add a word plane, then isomer will only generate planar clusters under the point group symmetry!
Point group |
Note |
|---|---|
|
Like |
|
Like |
|
Like |
|
Like |
|
Like |
|
Like |
|
Like |
|
The \(\mathrm{HClO}\) symmetry. |
|
The inversion symmetry. |
|
A symmetry weaker than \(\mathrm{CH}_4\). |
|
A symmetry weaker than \(\mathrm{CH}_4\). |
|
The \(\mathrm{CH}_4\) symmetry. |
|
A symmetry weaker than \(\mathrm{SF}_6\). |
|
The \(\mathrm{SF}_6\) symmetry. |
|
A symmetry weaker than \(\mathrm{C}_{60}\). |
|
The \(\mathrm{C}_{60}\) symmetry. |
5.4.2. Example: Au20 under Point Group Symmetries
Tip
The sample input and output files can be found in testfiles/isomer/5-pointgroup.
We want to build clusters of \(\mathrm{Au}_{20}\). If you just use cube to do global optimization, it may take you 100 steps to find the famous T d symmetry global minimum. Using point group grammar, you can quickly get a lot clusters with the assigned symmetry.
Prepare the following file au20.inp to generate \(\mathrm{Au}_{20}\) of D2d symmetry.
For Windows users, the content should be:
1au20 # Result file name
2Au 20 # Symbols
3D2d 2 2 2 # Structure types
410 # Maximal number of calculations
5>>>>
6copy $inp$ $out$
7>>>>
For Linux users, the content should be:
1au20 # Result file name
2Au 20 # Symbols
3D2d 2 2 2 # Structure types
410 # Maximal number of calculations
5>>>>
6cp $inp$ $out$
7>>>>
Here, copy $inp$ $out$ or cp $inp$ $out$ means just guess cluster structures without further optimization. Of course, you can change them to use Gaussian or xTB or others for optimization. Just run this:
isomer au20.inp > au20.out
In au20-LM, you will find that all structures have D 2d symmetry!
You can also try the following commands:
C5v 2 2 2Generate clusters under C 5v symmetry.C5h 2 2 2Generate clusters under C 5h symmetry.C5h 2 2 2 planeGenerate planar clusters under C 5h symmetry.Td 2 2 2Generate clusters under T d symmetry.Oh 2 2 2Generate clusters under O h symmetry.
For each of the point groups given above, we show an example here:
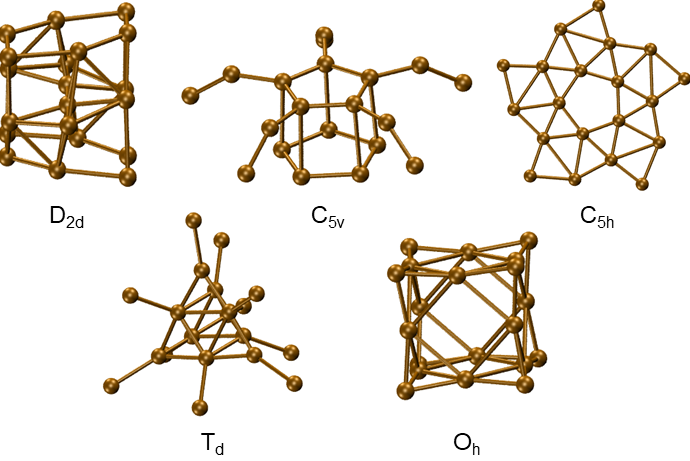
5.4.3. Example: B6N6
Tip
The sample input and output files can be found in testfiles/isomer/6-b6n6-xTB.
We want to know what a planar \(\mathrm{B}_{6}\mathrm{N}_{6}\) looks like in a C3h symmetry? This can be done easily with xTB and isomer. Prepare the following input:
1b6n6 # Result file name
2B 6 N 6 # Symbols
3C3h 1 1 1 plane # Structure types
410 # Maximal number of calculations
5>>>>
6./runxTB.sh $inp$ $out$ $xxx$
7>>>>
Make sure that in runxTB.sh the command line is: --chrg 0 --gfn 2. Run the global optimization:
isomer b6n6.inp > b6n6.out
In the output file b6n6.out, you can find the following output:
1Reordered from low to high energy:
2===============================================================
3 # Energy Match-RMSD
4===============================================================
5 3 -25.18133725 0.00000000
6 2 -24.84570255 1.31315189
7 0 -24.79607559 1.04903840
8 1 -24.49640410 0.99841844
9===============================================================
All the 4 isomers are shown below:
Of course, the global minimum of \(\mathrm{B}_{6}\mathrm{N}_{6}\) may not be even planar, but here we demonstrate that you can control the cluster symmetry flexibly with ABCluster!
5.4.4. Example: I and Ih symmetry clusters of Au60
Now, we will use ABCluster to generate some Au60 clusters with I and Ih symmetry. Prepare the following input:
1auI # Result file name
2Au 60 # Symbols
3I 3 3 3 # Structure types
410 # Maximal number of calculations
5>>>>
6cp $inp$ $out$
7>>>>
So, we will generate 10 clusters with I symmetry without using any external software. Run the global optimization:
isomer auI.inp > auI.out
Note that I and Ih symmetry are very similar. Due to some numerical issues, ABCluster may generate I and Ih symmetry simultaneously. In auI-LM, you will find that many structures have exactly I symmetry, but some of them are of Ih symmetry, since Ih is a stronger symmetry than I. Nevertheles, auI-LM/4.xyz and auI-LM/8.xyz are indeed of exact I symmetry:
We can use xTB to optimize the structure of, say, auI-LM/4.xyz. Use the following command:
xtb auI-LM/4.xyz --chrg 0 --gfn 1 > 4.out
Attention
For metallic clusters, we must use --gfn 1 instead of --gfn 2!
The optimized structure is named as xtbopt.xyz and we can rename it to 4-opt.xyz. It still has I symmetry!
To generate Ih symmetry, just repalce I by Ih in the input file:
1auIh # Result file name
2Au 60 # Symbols
3Ih 3 3 3 # Structure types
410 # Maximal number of calculations
5>>>>
6cp $inp$ $out$
7>>>>
So, we will generate 10 clusters with Ih symmetry without using any external software. Run the global optimization:
isomer auIh.inp > auIh.out
In auIh-LM, you will find that auIh-LM/0.xyz, auIh-LM/6.xyz, and auIh-LM/7.xyz are both of Ih symmetry. However, after optimization using xTB, we find that auIh-LM/0.xyz lose all symmetries, while auIh-LM/6.xyz and auIh-LM/7.xyz preserves Ih symmetry:
Thus, while ABCluster is able to preserve symmetry, some external software may lose symmetry in geometry optimization. This is a general issue in quantum chemistry calculations. However, clusters of the highest symmetry are NOT necessarily the lowest energy structures! In many cases, clusters with low or no symmetry may be the global minima!