Energy Decomposition Analysis

This tutorial will lead you step by step to do energy decomposition analysis (EDA) using Qbics. Currently, EDA can only be used with DFT.

Hint

If you use Qbics to do EDA in you paper, please cite the following references:

Example: EDA for (H₂SO₄)(NH₃)

Here, we will do an EDA for the molecular dimer (H₂SO₄)(NH₃). The input is given below:

1s1n.inp

basis
    def2-svp
end

scf
    charge     0
    spin2p1    1
    type       U # This is needed for EDA.
end

grimmedisp
    type bj       # Options: none, zero, bj.
end

eda
    type      tso
    frag  0 1 1-7
    frag  0 1 8-11
end

mol
    S                 -0.62161000   -0.11181000    0.09167200
    O                  0.03138700   -0.14316200    1.35576500
    O                 -1.82120800   -0.82692400   -0.15912300
    O                  0.38678100   -0.46814500   -1.02324300
    O                 -0.91128600    1.43385100   -0.17168300
    H                  1.34667100   -0.25497400   -0.71202200
    H                 -1.58729700    1.50230600   -0.85583700
    N                  2.78190500    0.03915200   -0.05091700
    H                  3.20716100    0.92239700   -0.30232700
    H                  3.46881800   -0.69082400   -0.19060100
    H                  2.55167500    0.07103700    0.93671700
end

task
   eda b3lyp
end

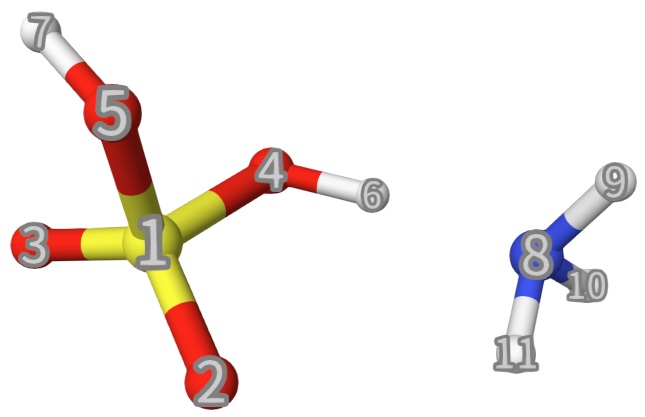
Line 8: For EDA, you must explicitly set the type to U in scf...end.
Line 16: Do TSO-type EDA. You can also use gks to do generalized Kohn-Sham (GKS) type EDA.
Line 17-18: The fragments in EDA. Each line defines the charge, spin multiplicity, and atom indices. See below:

After running this calculation, we have the following output:

1s1n.out

WITHOUT BSSE correction:
Electrostatic interaction energy:                 -30.95 kcal/mol
Exchange-correlation interaction energy:           27.55 kcal/mol
Polarization interaction energy:                   -5.44 kcal/mol
Charge transfer interaction energy:               -15.25 kcal/mol
Grimme's dispersion interaction:                   -2.22 kcal/mol
----------------------------------------------------------------
Total interaction energy:                         -26.31 kcal/mol

WITH BSSE correction:
Electrostatic interaction energy:                 -30.95 kcal/mol
Exchange-correlation interaction energy:           27.55 kcal/mol
Polarization interaction energy:                   -5.44 kcal/mol
Charge transfer interaction energy:               -10.44 kcal/mol
Grimme's dispersion interaction:                   -2.22 kcal/mol
----------------------------------------------------------------
Total interaction energy:                         -21.50 kcal/mol

In this output, the interaction energy of the following process

H₂SO₄ + NH₃ = (H₂SO₄)(NH₃)

is decomposed into several components. The interaction energy WITH and WITHOUT BSSE is -21.50 kcal/mol and -26.31 kcal/mol. The BSSE energy is included in Charge transfer interaction energy.

The Electrostatic interaction energy, Polarization interaction energy and Charge transfer interaction energy are all stablizing the dimer, the first contributing most. The Exchange-correlation interaction energy can also be recognized as Pauli exclusion energy, which destablizing the dimer.

For different kinds of molecular dimer, the weights of different components are quiet different, indicating the nature of chemical interactions.

Example: EDA for (Ca²⁺)(SO₄^2-)(H₂O)₅ 

The basic MB-EDA formular is:

\[\Delta E^{\text{int}} = \frac{1}{2!} \sum_{I_1 \neq I_2}^{N} \Delta E_{I_1 I_2}^{(2)} +\frac{1}{3!} \sum_{I_1 \neq I_2 \neq I_3}^{N} \Delta E_{I_1 I_2 I_3}^{(3)} + \cdots + \frac{1}{n!} \sum_{I_1 \neq \cdots \neq I_n}^{N} \Delta E_{I_1 \cdots I_n}^{(n)} + \cdots + \Delta E_{I_1 \cdots I_N}^{(N)} \equiv \sum_{n=2}^{N} \Delta E^{(n)}\]

The terms higher than \(\Delta E^{(2)}\) is the many-body interaction term. Usually the most important one is the three-body effect \(\Delta E^{(3)}\), the effects of which can be decomposed into three ones:

\(\Delta E^{(3)} < 0\): Indicate a cooperative effect of the monomers in a cluster. The many-body interaction is stabilizing the cluster. This is often seen in hydrogen bonding clusters, like water clusters.
\(\Delta E^{(3)} > 0\): Indicate an anti-cooperative effect of the monomers in a cluster. The many-body interaction is destabilizing the cluster. This is often seen in a cluster of charged species, like ionic liquid clusters. Also see below.
\(\Delta E^{(3)} \approx 0\): Indicate a non-cooperative effect of the monomers in a cluster. There is little many-body interaction in the cluster. This is often seen in a cluster of molecules without charges or hydrogen bonds.

Each order can be decomposed into electrostatic, exchange, polarization, charge transfer, and dispersion terms:

\[\Delta E_X^{(n)} = \Delta E_X^{(n)\text{-el}} + \Delta E_X^{(n)\text{-ex/xc}} + \Delta E_X^{(n)\text{-pl}} + \Delta E_X^{(n)\text{-ct}} + \Delta E_X^{(n)\text{-disp}}\]

Usually, electrostatic and exchange terms are highly additive, while polarization and charge transfer terms are non-additive. The dispersion term is always additive.

Here we will do an EDA for the microsolvated cluster (Ca²⁺)(SO₄^2-)(H₂O)₅. Since there are more than 2 species, we will use many-body EDA (MB-EDA) to decompose the interaction energy components into contributions from different many-body level. Usually, contributions beyond three-body are very small, so we will truncate the computation at four-body.

The input is given below:

caso4h2o5.inp

basis
    def2-svp
end

scf
    charge     0
    spin2p1    1
    type       U # This is needed for EDA.
end

grimmedisp
    type bj
end

eda
    type     mb_tso
    mb_level 4  # The many-body truncation level.
    frag  +2 1 1
    frag  -2 1 2-6
    frag   0 1 7-9
    frag   0 1 10-12
    frag   0 1 13-15
    frag   0 1 16-18
    frag   0 1 19-21
end

mol
   Ca      1.98604937      1.24582501      1.89905383
    S      0.69103489      3.45226578      0.98237460
    O      2.08708072      3.44779165      1.50308184
    O      0.24826049      2.05102931      0.73622996
    O     -0.21032250      4.08940001      1.98323165
    O      0.63912085      4.22084216     -0.29304506
    O      3.02175028      0.83377391     -0.05175855
    H      3.13194669      0.09601115     -0.65158745
    H      2.90415260      1.59241194     -0.62348488
    O      2.51307423      2.92493798     -1.72944079
    H      1.80535522      3.44397361     -1.34738364
    H      2.91500306      3.50585612     -2.37536585
    O      0.60914213     -0.51387571      1.58896733
    H      0.07645358     -1.26917200      1.83796991
    H      0.01571971      0.04244367      1.08439778
    O      0.73702072      1.93958625      3.70546127
    H      0.73393089      2.03509947      4.65787899
    H      0.20818330      2.67203308      3.38909995
    O      3.87639195      1.93942131      2.91131853
    H      4.78820918      1.95286631      3.20224881
    H      3.69756418      2.83995160      2.64058309
end

task
   eda b3lyp
end

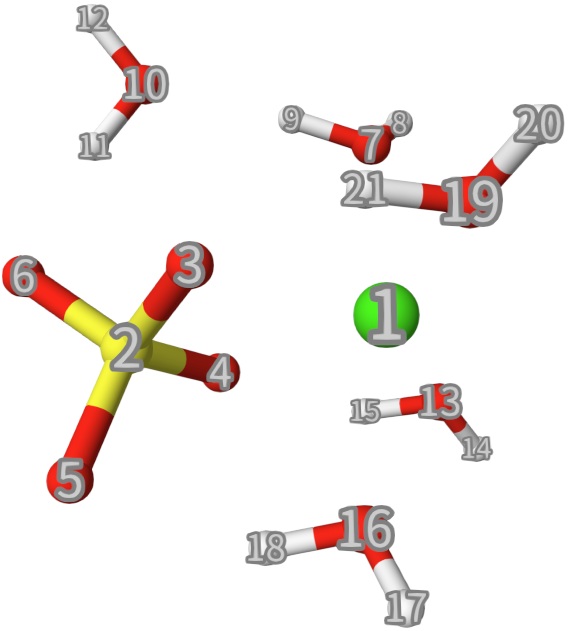
Line 16: To do MB-EDA, you should use mb_tso.
Line 17: mb_level 4 means you truncate the MB-EDA at four-body.
Line 18-24: Set 7 chemical fragements. Note that some species like Ca²⁺ and SO₄^2- are charged. You should give the correct charge.

The atomic indices are shown below:

After running this calculation, we have the following output:

caso4h2o5.out

Table 5. Summary (kcal/mol).
---------------------------------------------------------------------------------------------------------------------------------
    Interactions         delE_el         delE_xc         delE_pl         delE_ct       delE_bsse       delE_disp        delE_tot
---------------------------------------------------------------------------------------------------------------------------------
   SUM of 2-body -6.73148230E+02  1.47696370E+02 -1.11395126E+02 -2.04547116E+02  1.03684957E+02 -2.06082308E+01 -7.58317375E+02
   SUM of 3-body  1.42501290E-08 -2.67700179E+00  6.09855572E+01  1.30716087E+02 -4.86421459E+01  1.07484123E+01  1.51130908E+02
   SUM of 4-body -2.82504918E-08  5.22296932E-01 -4.66678754E+00 -4.78862109E+01  1.47634652E+01 -1.52639538E+01 -5.25311901E+01
          Remain  1.63009297E-08 -9.27025377E-02  2.21610464E-01  1.02616142E+01 -2.89029982E+00  7.47122033E+00  1.49714426E+01
---------------------------------------------------------------------------------------------------------------------------------
             SUM -6.73148230E+02  1.45448963E+02 -5.48547462E+01 -1.11455626E+02  6.69159769E+01 -1.76525519E+01 -6.44746214E+02
---------------------------------------------------------------------------------------------------------------------------------

We can see that the total interaction energy is -644.75 kcal/mol, which is decomposed into 2-body, 3-body, 4-body, and remaining terms. The 2-body term is the most important one (-758.32 kcal/mol), while the 3-body term is also significant but anti-cooperative (destablizing the cluster) (+151.13 kcal/mol). The 4-body term is small (-52.53 kcal/mol, slightly cooperative). The remaining term (sum of 5-, 6-, and 7-body) is very small (+14.97 kcal/mol) compared to the low-order terms.

We can also see that the electrostatic and exchange energy are highly additive (beyond 3-body is almost zero), while the polarization and charge-transfer energy are non-additive:

Type	2-body	3-body	4-body	Total
Polarization	-111.40 kcal/mol	+60.99 kcal/mol	-4.67 kcal/mol	-54.85 kcal/mol
Charge transfer	-204.55 kcal/mol	+130.72 kcal/mol	-47.89 kcal/mol	-111.45 kcal/mol

For different kinds of clusters, the 3-body effects (many-body interactions) can be quite different, see Phys. Chem. Chem. Phys. 2024, 26, 17549 for more information.

Energy Decomposition Analysis

Example: EDA for (H2SO4)(NH3)

Example: EDA for (Ca2+)(SO42-)(H2O)5

Example: EDA for (H₂SO₄)(NH₃)

Example: EDA for (Ca²⁺)(SO₄^2-)(H₂O)₅ 