Tip

All input files can be downloaded: Files.

Tip

For more information of this section, please refer to these keywords:

scf
scfguess

TSO-DFT (2): Diabatic States

This tutorial will lead you step by step to do target state optimization DFT (TSO-DFT) using Qbics. TSO-DFT is an originally developed method in Qbics. It is a powerful and accurate method for excited and diabatic states. In many physical processes like charge transfer, TSO-DFT can give much more reasonable results than TDDFT. Therefore, it is worth learning this method.

Hint

If you use Qbics to do TSO-DFT in you paper, please cite the following references:

J. Chem. Theory Comput. 2023, 19, 1777

In this tutorial, we will introduce how to use TSO-DFT to study dibatic states.

Example: Definition of Diabatic States of NaCl 

What is a diabatic state? Its exact definition can be found in textbooks but are not relevant to us here. Here we just use an example to show what a diabatic state is. We will take NaCl molecule as an example.

Adiabatic State 

We will calculate the ground state of NaCl at B3LYP/def2-TZVP level of theory:

nacl-1.inp

basis
    def2-tzvp
end

scf
    charge  0
    spin2p1 1
    type    U
end

mol
   Na      0.0   0.0   -0.68381052
   Cl      0.0   0.0    1.68381052
end

task
    energy b3lyp
end

Let us check the Mulliken charges in nacl-1.out:

nacl-1.out

Mulliken Populations
====================
     #  Symbol          Charge            Spin
----------------------------------------------
     1      Na      0.64773687     -0.00000889
     2      Cl     -0.64773687      0.00000889
----------------------------------------------
   Sum             -0.00000000      0.00000000
----------------------------------------------
...omitted...
Final total energy:        -622.60503718 Hartree

Therefore, the Mulliken charges are 0.6477 and -0.6477, respectively, so the charges are delocalzied over the whole molecule. This state is also called adiabatic state.

Diabatic State: [Na⁺][Cl^-]

Intuitively, one may think that NaCl is composed of a sodium cation Na⁺ and a chloride antion Cl^-. However, as shown above, in the adiabatic state, charges are delocalized over the molecule. Is it possible to calculate a state that charges are forced to localize on some atoms? Such state is called diabatic state. In the following, we will calculate a diabatic state of [Na⁺][Cl^-]:

nacl-2.inp

basis
    def2-tzvp
end

scf
    charge  0
    spin2p1 1
    type    U   # This is needed for TSO-DFT.
    no_scf  tso
end

scfguess
    type fragden
    frag +1 1 1
    frag -1 1 2
end

mol
   Na      0.0   0.0   -0.68381052
   Cl      0.0   0.0    1.68381052
end

task
    energy b3lyp
end

You can see that, in scfguess...end, we are setting a superposition of fragment density (fragden) as SCF initial guess. The only difference is that we set no_scf tso in scf...end:

frag +1 1 1 We are seeting the fragment of atom 1 with charge +1 and spin multiplicity 1. See scfguess for details.
frag -1 1 2 We are seeting the fragment of atom 2 with charge -1 and spin multiplicity 1.

After calculation, in nacl-2.out, we can find this:

nacl-2.out

Mulliken Populations
====================
     #  Symbol          Charge            Spin
----------------------------------------------
     1      Na      1.00000000      0.00000000
     2      Cl     -1.00000000     -0.00000000
----------------------------------------------
   Sum             -0.00000000     -0.00000000
----------------------------------------------
...omitted...
Final total energy:        -622.58940107 Hartree

Indeed, at Na and Cl atom, the Mulliken charge is 1.00 and -1.00, respectively, in line with our assumed diabatic state [Na⁺][Cl^-]. Its is higher than the adiabatic state by

-622.58940107 - (-622.60503718) = 0.0156 Hartree = 9.81 kcal/mol

Actually, this is the so-called charge-transfer interaction energy. By the way, if you check the SCF process of this diabatic state:

nacl-2.out

  #it           SCF energy            2e energy    |deltaE|    |deltaP| Orbital  Time/second
---------------------------------------------------------------------------------------------
    1        -622.57645781         318.90071152   1.950E-01   1.100E-05   guess        0.046
    2        -622.58412894         319.42032296   7.671E-03   3.461E-05    diis        0.054
    3        -622.58935124         319.21103043   5.222E-03   3.376E-05    diis        0.052
    4        -622.58939707         319.19096764   4.584E-05   5.708E-06    diis        0.052
    5        -622.58939958         319.18902943   2.506E-06   9.746E-07    diis        0.051
    6        -622.58940082         319.19159833   1.235E-06   3.969E-07    diis        0.053
    7        -622.58940107         319.19461843   2.492E-07   9.841E-08    diis        0.052
---------------------------------------------------------------------------------------------
 Great (^ _ ^) SCF has converged in 7 iterations. (0.367 seconds)

The energy difference of the first and last cycle

-622.58940107 - (-622.57645781) = 0.0129 Hartree = 8.12 kcal/mol

is the so-called polarization interaction enerrgy.

Energy Decomposition Analysis of [Na⁺][Cl^-]

To check this, if you do an EDA (see Energy Decomposition Analysis) for [Na⁺][Cl^-] with the following input:

nacl-eda.inp

basis
    def2-tzvp
end

scf
    charge  0
    spin2p1 1
    type    U   # This is needed for TSO-DFT.
end

eda
    type tso
    frag +1 1 1
    frag -1 1 2
end

mol
   Na      0.0   0.0   -0.68381052
   Cl      0.0   0.0    1.68381052
end

task
    eda b3lyp
end

In the output nacl-eda.out:

nacl-eda.out

WITHOUT BSSE correction:
Electrostatic interaction energy:                -146.30 kcal/mol
Exchange-correlation interaction energy:           23.91 kcal/mol
Polarization interaction energy:                   -8.12 kcal/mol
Charge transfer interaction energy:                -9.81 kcal/mol
Grimme's dispersion interaction:                    0.00 kcal/mol
----------------------------------------------------------------
Total interaction energy:                        -140.33 kcal/mol

Here, Charge transfer interaction energy: -9.81 kcal/mol and Polarization interaction energy: -8.12 kcal/mol confirm our previous calculations.

Diabatic State: [Na][Cl]

Besides [Na⁺][Cl^-], we can also assume another diabatic state: NaCl is composed of 2 neutral radical:

nacl-3.inp

basis
    def2-tzvp
end

scf
    charge  0
    spin2p1 1
    type    U   # This is needed for TSO-DFT.
    no_scf  tso
end

scfguess
    type fragden
    frag 0  2 1
    frag 0 -2 2
end

mol
   Na      0.0   0.0   -0.68381052
   Cl      0.0   0.0    1.68381052
end

task
    energy b3lyp
end

Here, frag 0 2 1 means that Na has a single alpha electron, while frag 0 2 1 means that Cl has a single beta electron, like this:

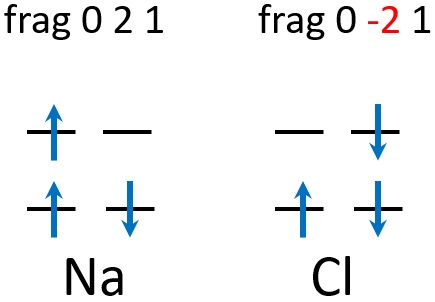
After calculation, we can find this in nacl-3.out:

nacl-3.out

---------------------------------------------------------------------------------------------
  #it           SCF energy            2e energy    |deltaE|    |deltaP| Orbital  Time/second
---------------------------------------------------------------------------------------------
    1        -622.42824748         316.12630594   3.002E-02   3.077E-04   guess        0.051
    2        -622.43470909         315.62361860   6.462E-03   2.354E-04    diis        0.063
    3        -622.43589868         315.69293084   1.190E-03   2.159E-05    diis        0.057
    4        -622.43598379         315.69186515   8.511E-05   2.740E-05    diis        0.059
    5        -622.43599795         315.67167823   1.417E-05   5.266E-07    diis        0.057
    6        -622.43600008         315.68068350   2.120E-06   9.311E-06    diis        0.071
    7        -622.43600052         315.68009817   4.407E-07   5.151E-07    diis        0.057
---------------------------------------------------------------------------------------------
...omitted...
Mulliken Populations
====================
     #  Symbol          Charge            Spin
----------------------------------------------
     1      Na     -0.00000000      0.50000000
     2      Cl      0.00000000     -0.50000000
----------------------------------------------
   Sum             -0.00000000     -0.00000000
----------------------------------------------
...omitted..
Final total energy:        -622.43600052 Hartree

So, the polarization and charge transfer interaction energy is:

-622.43600052 - (-622.42824748) Hartree = -4.88 kcal/mol

-622.60503718 - (-622.43600052) Hartree = -106.07 kcal/mol

Compared with [Na⁺][Cl^-], the charge transfer energy of [Na][Cl] is extremely high.

You can also try to compute a diabatic state of [Na^-][Cl⁺] if you wish.

In practise, to study diabatic states of molecular dimer or clusters, you can simply use eda since all needed calculations will be done automatically. You just need to set the fragment charges and spin multiplicities.

Example: Reactant and Product Diabatic States of F^-+CH₃Cl 

Reactant Complex 

Now we consider the reaction F^-+CH₃Cl. First, we calculate the reactant complex. Now we calculate the reactant and product diabatic state:

fch3cl-reac-reac.inp

basis
    def2-svp
end

scf
    charge  0
    spin2p1 -1
    type    U   # This is needed for TSO-DFT.
    no_scf  tso
end

scfguess
    type fragden
    frag  0 1 1-5
    frag -1 1 6
end

mol
  C                 -0.43654823    1.13197968    0.00000000
  H                 -0.07987539    1.63637787    0.87365150
  H                 -0.07987539    1.63637787   -0.87365150
  H                 -1.50654823    1.13199286    0.00000000
 Cl                  0.15009830   -0.52737135    0.00000000
  F                 -1.63124586    2.75454539   -0.44024554
end

task
    energy b3lyp
end

fch3cl-reac-prod.inp

basis
    def2-svp
end

scf
    charge  0
    spin2p1 -1
    type    U   # This is needed for TSO-DFT.
    no_scf  tso
end

scfguess
    type fragden
    frag  0 1 1-4 6
    frag -1 1 5
end

mol
  C                 -0.43654823    1.13197968    0.00000000
  H                 -0.07987539    1.63637787    0.87365150
  H                 -0.07987539    1.63637787   -0.87365150
  H                 -1.50654823    1.13199286    0.00000000
 Cl                  0.15009830   -0.52737135    0.00000000
  F                 -1.63124586    2.75454539   -0.44024554
end

task
    energy b3lyp
end

The two dibatic states can be set using frag:

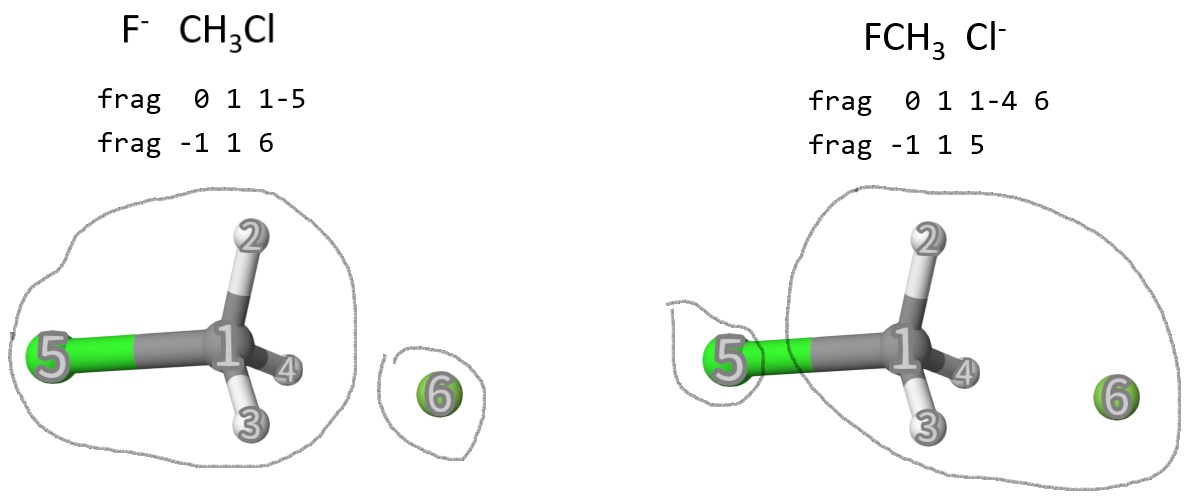
Transition State 

In the same way, we calculate the reactant and product diabatic states, but at the transition state:

fch3cl-ts-reac.inp

basis
    def2-svp
end

scf
    charge  0
    spin2p1 -1
    type    U   # This is needed for TSO-DFT.
    no_scf  tso
end

scfguess
    type fragden
    frag  0 1 1-5
    frag -1 1 6
end

mol
   C     -0.59663490      1.29366556     -0.07171644
   H     -0.18159761      1.68969864      0.84430018
   H     -0.12252870      1.52677601     -1.01427388
   H     -1.59298434      0.87532545     -0.06612308
  Cl      0.43269073     -0.72181312      0.13298792
   F     -1.52293997      3.10024978     -0.26542025
end

task
    energy b3lyp
end

fch3cl-ts-prod.inp

basis
    def2-svp
end

scf
    charge  0
    spin2p1 -1
    type    U   # This is needed for TSO-DFT.
    no_scf  tso
end

scfguess
    type fragden
    frag  0 1 1-4 6
    frag -1 1 5
end

mol
   C     -0.59663490      1.29366556     -0.07171644
   H     -0.18159761      1.68969864      0.84430018
   H     -0.12252870      1.52677601     -1.01427388
   H     -1.59298434      0.87532545     -0.06612308
  Cl      0.43269073     -0.72181312      0.13298792
   F     -1.52293997      3.10024978     -0.26542025
end

task
    energy b3lyp
end

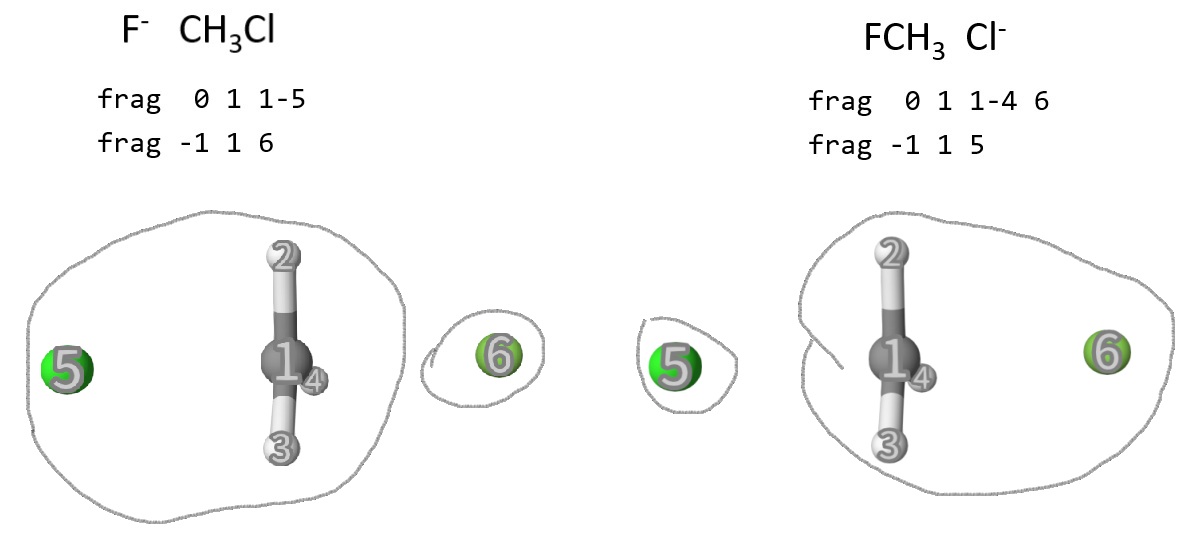
After 4 calculations, we can get the following energies in fch3cl-reac-reac/prod.out and fch3cl-ts-reac/prod.out:

Structure

Reactant Complex

Transition State

Reactant Dibatic State

-599.62530856

-599.62955746

Product Dibatic State

-599.49007047

-599.62959766

Interestingly, we observe that the reactant and product diabatic energy are the same for transition state. Acutally, this is the basis for dibatic MECP method for transition state search. See Transition State Search and mecp for more information.